Aeraulica e ventilazione: leggi e grandezze fisiche coinvolte
Le leggi fisiche alla base della movimentazione dei fluidi ed il funzionamento dei ventilatori
Aspirazione aria ed aeraulica – Leggi fisiche e ventilatori industriali
L’ambito dei processi produttivi risulta essere estremamente vario. È anche vero che la maggior parte delle produzioni sono accomunate da una necessità: la movimentazione dei fluidi. Infatti, se nei processi risulta necessario l’utilizzo di correnti liquide o gassose, devono esservi delle apposite apparecchiature che consentono il movimento di tali correnti.
Nel caso di nostro interesse, ossia quello del trattamento di inquinanti gassosi (polveri, particolato, COV, nebbie oleose, gas acidi, odori,…), le apparecchiature che consentono la movimentazione delle correnti aeriformi sono i ventilatori e aspiratori industriali.
L’obiettivo di questo articolo è quello di fornirti informazioni sulle leggi fisiche che stanno alla base della movimentazione dei fluidi e, dunque, del funzionamento dei ventilatori. In particolar modo analizzeremo:
- La legge di conservazione della massa
- La legge di conservazione dell’energia
- Un esempio pratico, per vedere come queste leggi governano il moto di un flusso aeriforme all’interno di una tubazione
Leggi fisiche
Consideriamo un fluido che si muove in una determinata tubazione. Su di esso possono essere applicati due importanti principi di conservazione: la conservazione della massa e la conservazione dell’energia.
La conservazione della massa
Il principio di conservazione della massa ci dice che la quantità totale di materia che fluisce a stazionario all’interno del condotto, a patto che non vi siano alimentazioni secondarie o perdite, è costante. Applicando questa legge a due diverse sezioni della tubazione (che chiameremo 1 e 2), e tenendo conto del fatto che una portata massiva può essere scritta come prodotto tra densità (ρ) e portata volumetrica, otteniamo:
Questa legge ci mostra una cosa molto importante: se le densità nelle due sezioni risultano circa uguali, allora anche la portata volumetrica del fluido tende ad essere la stessa. Affermare che la densità è circa uguale, visto che stiamo parlando di un flusso gassoso, vuol dire considerare delle variazioni non significative di pressione e di temperatura.
Possiamo fare un passo in più, notando che una portata volumetrica può essere espressa come prodotto tra la velocità (v) e la sezione di attraversamento (A) del fluido. Tenendo conto di questo, l’equazione diventa:
Da qui deduciamo un altro elemento importante: se la densità è circa costante e la sezione della tubazione non modifica il suo valore, allora anche la velocità del fluido risulta la medesima nelle due sezioni. Questo è un aspetto molto importante, che ci servirà nelle successive considerazioni. L’altro principio di cui ci avvaliamo è la conservazione dell’energia.
La conservazione dell’energia
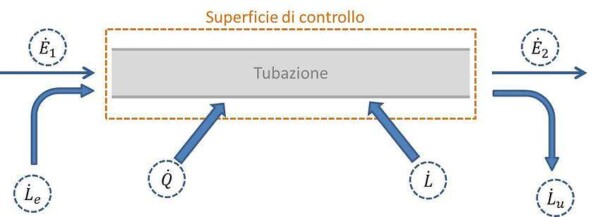
All’interno della superficie di controllo, che circonda la tubazione, entrano ed escono diverse potenze:
- E: questa tipologia di potenza è associata ai flussi massivi entranti e uscenti. In particolar modo, ciascun flusso massivo porta dei contributi energetici specifici legati all’energia interna del flusso (u), alla sua energia potenziale gravitazionale (gz, dove g è l’accelerazione di gravità e z è la quota rispetto ad un sistema di riferimento) e alla sua energia cinetica (1/2v2). Dunque:
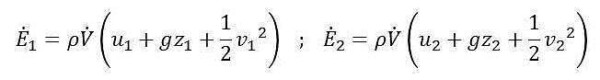
- Le e Lu: Sono i contributi energetici legati al lavoro di pompaggio. La portata massiva entrante viene pompata dentro la superficie di controllo dal fluido che la precede, mentre la portata massiva uscente viene pompata fuori dalla superficie di controllo dal fluido presente nella tubazione stessa. Questi contributi possono essere quantificati come prodotto tra la pressione alla sezione considerata (p) e la portata volumetrica del fluido.
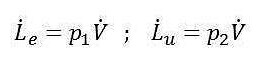
- Q: Rappresenta la potenza termica entrante o uscente dalla tubazione. È tipicamente considerata positiva quando entrante.
- L: Rappresenta la potenza entrante o uscente dalla tubazione in conseguenza all’azione di forze superficiali, volumetriche o derivanti da apparecchiature meccaniche appositamente inserite. Viene tipicamente considerata positiva quando entrante, anche se per alcuni specifici contesti può essere utilizzata la convenzione opposta.
Considerando una situazione stazionaria, in cui il quantitativo energetico complessivo presente all’interno della tubazione non varia, si ha che la somma delle potenze entranti deve uguagliare la somma delle potenze uscenti. Dunque:
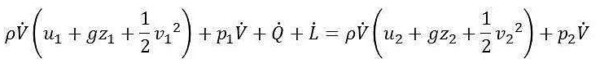
Introduciamo ora una serie di ipotesi semplificative:
- Assenza di scambi termici (Q=0). Dal momento che il gas non scambia calore con l’esterno, la sua temperatura risulterà essere uniforme. Poiché, inoltre, l’energia interna di un gas perfetto (a cui l’aria può essere approssimata) è funzione della sola temperatura, abbiamo che l’energia interna in corrispondenza delle due sezioni sarà la medesima. Possiamo dunque semplificarla all’interno del bilancio.
- Assenza di potenza associata al lavoro di forze superficiali, volumetriche o legate ad apparecchiature meccaniche. Non vengono conteggiati in questa ipotesi le forze di pressione (già prese in considerazione in Le e Lu) e quelle associate agli sforzi viscosi. In particolar modo, gli sforzi viscosi danno origine ad un contributo di potenza negativo. Chiamiamo questo contributo Lτ, e conferiamogli segno negativo per mettere in evidenza il fatto che è un contributo uscente.
Il bilancio di energia assume così la seguente forma:
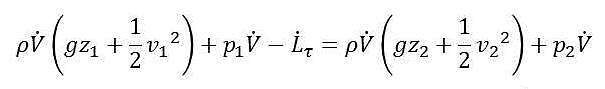
Dividiamo ora entrambi i membri dell’equazione per la portata volumetrica, e spostiamo il termine legato agli sforzi viscosi a destra dell’uguale:
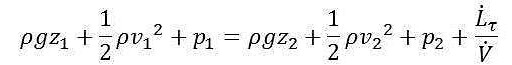
L’equazione ora ricavata è di fondamentale importanza. I tre termini che compaiono a sinistra dell’uguale e i primi tre termini che compaiono a destra dell’uguale rappresentano i termini di Bernoulli nelle condizioni di ingresso e di uscita. Il famoso teorema di Bernoulli afferma che la somma di questi tre termini, nel caso di moto di un fluido ideale (con assenza di fenomenologie di attrito), si conserva. Nel nostro caso questa idealizzazione non è vera dal momento che abbiamo tenuto conto del contributo legato alle dissipazioni viscose, che tendono a far diminuire il quantitativo energetico complessivo. In particolar modo, il rapporto tra potenza dissipata per attrito e portata volumetrica è a livello dimensionale uguale ad una pressione:
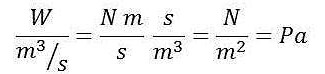
Tale rapporto corrisponde alle perdite di carico all’interno della tubazione, e lo chiameremo pc. Questa grandezza dipende tipicamente sia dalle proprietà del fluido (densità e viscosità) che dalle caratteristiche costruttive e fluidodinamiche del sistema.
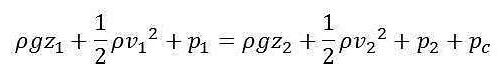
Un esempio pratico di calcolo
Ok, fino ad ora il discorso è stato teorico. Quali sono le conseguenze dal punto di vista pratico? Per capirlo, immaginiamo la seguente situazione.

Immaginiamo di avere una tubazione caratterizzata da una sezione costante (pari ad A), e di voler far fluire attraverso essa una determinata portata di gas. Abbiamo visto che, se gli scambi termici sono nulli e se le variazioni di pressione sono esigue (rispetto alla pressione totale, come spesso avviene per le perdite di carico), la densità della corrente gassosa risulta uniforme, e di conseguenza risulta uniforme anche la velocità:
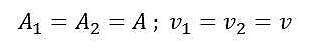
Ne consegue che i due termini cinetici presenti nell’equazione prima analizzata si semplificano tra di loro, e otteniamo:
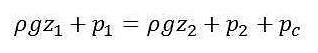
Ipotizzando trascurabile il contributo legato alla variazione di energia gravitazionale (questo vale per piccole variazioni di quota), possiamo scrivere che:
Questa equazione è di fondamentale importanza, perché ci mostra che in regime non ideale, affinché il fluido si muova, è necessario avere una differenza di pressione (pari alle perdite di carico) tra le due sezioni. In particolar modo, fluirà nella tubazione una portata volumetrica di fluido che dà luogo a delle perdite di carico esattamente uguali alla differenza di pressione tra le due estremità.
Per generare queste differenze di pressione vengono utilizzati, appunto, i ventilatori. Nel prossimo articolo esamineremo le varie grandezze fisiche che caratterizzano il funzionamento dei ventilatori e quali criteri vengono utilizzati per operarne la scelta.
Nel frattempo, esamina le nostre Case History per vedere come Tecnosida® utilizza impianti di aspirazione nelle sue realizzazioni!
A presto!